5 Exercícios Resolvidos sobre Gráfico e Estudo completo de Funções Modulares

GRÁFICO E ESTUDO COMPLETO DE FUNÇÕES MÓDULOS/ MODULARES

O que é função modular?

Uma função modular é aquela em que na sua lei de definição, possui uma variável dentro do módulo. As funções modulares podem ser do tipo: y=|f(x)|  ou y=f(|x|)

Exemplos: $f(x)=|x-1|;$ $g(x)=|x^2-1|;$ $h(x)=x^2-2|x|$

Como é um gráfico de uma função modular? 

O gráfico de uma função módulo do tipo y=|f(x)|  é sempre uma reflexão, em torno do eixo x, dos pontos do gráfico de y=f(x) que possuem ordenada negativa. 

E o gráfico de uma função módulo do tipo y=f(|x|)é sempre uma reflexão, em torno do eixo y, dos pontos do gráfico de y=f(x) que possuem abcissa negativa.

EXERCÍCIOS RESOLVIDOS

Construa o gráfico e faca o estudo completo, em:

1) f(x)=|x-3|

Gráfico 

Para construir o gráfico da função $f(x)=|x-3|$ podemos nos basear nos seguintes passos:

1º Passo: Construir o gráfico (tracejado) de $y=x-3:$
Lembre-se que: o gráfico de y=x-3 é obtido pelos seguintes pontos de $y=ax+b:$
$x-3=0$  ⇔   $x=0+3$  ⇔  $x=3$ e a ordenada na origem é o valor de $y=b=-3$

2º Passo: Construir o gráfico de f(x)=|x-3| através de uma simetria em relação ao eixo das abcissas (eixo x)
-- Isto significa uma reflexão, em torno do eixo x, dos pontos do gráfico que possuem ordenada negativa.

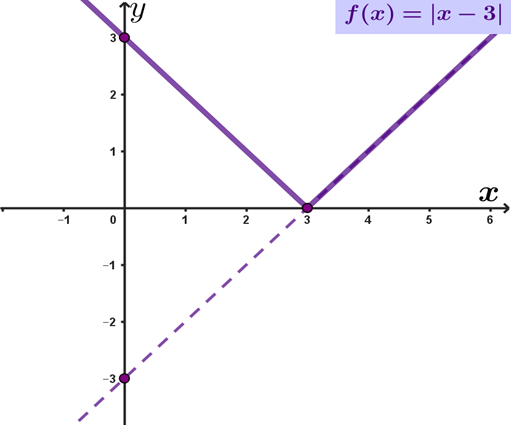
Estudo completo:

 

Domínio: Df=x∈R

Contradomínio: D'f=y∈[0; +∞[

Zeros: x={3}

A ordenada na origem é 3

Vértice: (3;0)

Eixo de simetria: x=3

Monotonia:

- É decrescente em x∈]-∞; 3[

- É crescente em x∈]3; +∞[

Variação do sinal 

- A função é positiva em x∈R\{3}

- A função é nula (=0) em x={3}

- A função não tem parte negativa.

-----------------------

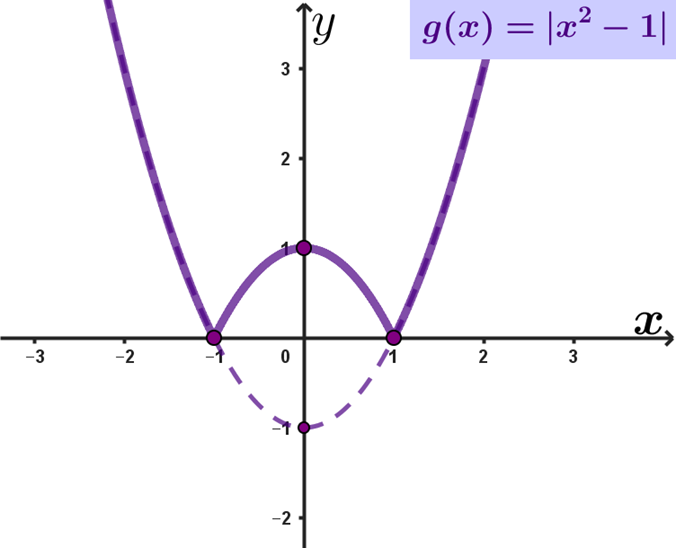
$2) g(x)=|x^2-1|$

Gráfico:

Para construir o gráfico da função g(x)=| $x^2-1$ |podemos nos basear nos seguintes passos:

1º Passo: Construir o gráfico (tracejado) de $y=x^2-1$:

Lembre-se que: o gráfico de $y=x^2-1$ é obtido pelos seguintes pontos da função $$y=ax^2+bx+c:$$ $x^2-1=0$  ⇔  $x^2=1$  

⇔  $x=± \sqrt{1}$   ⇔  $x=±1$ 

 ⇔  $x_1=-1 ∨ x_2=1$ 

E a ordenada na origem é $y=c=-1.$

2º Passo: Construir o gráfico de g(x)=|$x^2-1$| através de uma simetria em relação ao eixo das abcissas (eixo x)

-- Isto significa uma reflexão, em torno do eixo x, dos pontos do gráfico que possuem ordenada negativa.

Estudo completo:

 

Domínio: Dg=x∈R

Contradomínio: $D'g=y∈R_0^+$ ou $D'g=y∈[0; +∞[$

Zeros: x={-1; 1}

A ordenada na origem é 1

Vértices: $V_1 (-1;0);V_2 (0;1);V_3 (1;0)$

Eixo de simetria: x=3

Monotonia:

- É decrescente em x∈]-∞;-1[ ∪ ]0;1[ 

- É crescente em x∈]-1;0[ ∪ ]1;+∞[

Variação do sinal 

- A função é positiva em x∈R\{-1;1}

- A função é nula (=0) em x={-1;1}

- A função não tem uma parte negativa.

 -----------------------

3) $h(x)=x^2-2|x|$

Gráfico

Para construir o gráfico da função $h(x)=x^2-2|x|$ podemos nos basear nos seguintes passos:

1º Passo: Construir o gráfico (tracejado) de $y=x^2-2x:$

Lembre-se que: o gráfico de $y=x^2-2x$ é obtido pelos seguintes pontos da função $y=ax^2+bx+c:$ 

Resolvendo temos: $x_1=1 ∨x_2=2; x_V=1; y_V=-1$ e a ordenada na origem é o valor de $y=c=0$

2º Passo: Construir o gráfico de $h(x)=x^2-2|x|$  através de uma simetria em relação ao eixo das ordenadas (eixo y)

-- Isto significa fazer uma reflexão, em torno do eixo y, dos pontos do gráfico que possuem abcissa negativa.

Estudo completo:

 

Domínio: Dh=x ∈ R

Contradomínio: D'h=y ∈ [-1; +∞[

Zeros: x={-2; 0; 2}

A ordenada na origem é 0

Vértices: $V_1 (-1;-1);V_2 (0;0);V_3 (1;-1)$

Eixo de simetria: x=0

Monotonia:

- É decrescente em

 x∈]-∞;-1[ ∪ ]0;1[ 

- É crescente em x∈]-1;0[ ∪ ]1;+∞[

Variação do sinal 

- A função é positiva em  x∈]-∞;-2[ ∪ ]2;+∞[ 

- A função é nula (=0) em x=\{-2;0;2}

- A função é negativa em  x∈]-2;2[ \{0}

4) i(x)=|x|+2

Gráfico

Para construir o gráfico da função i(x)=|x|+2 podemos nos basear nos seguintes passos:

1º Passo: Construir o gráfico (tracejado) de y=x+2:

Lembre-se que: o gráfico de $y=x+2$ é obtido pelos seguintes pontos de $y=ax+b:$

$x+2=0$  ⇔   $x=0-2$  ⇔  $x=-2$ e a ordenada na origem é o valor de y=b=2

2º Passo: Construir o gráfico de i(x)=|x|+2 através de uma simetria em relação ao eixo das ordenadas (eixo y)

-- Isto significa fazer uma reflexão, em torno do eixo y, dos pontos do gráfico que possuem abcissa negativa.

 

Estudo completo: 

Domínio: Di=x∈R

Contradomínio: D'i=y∈[2; +∞[

Zeros: não tem zeros:

A ordenada na origem é 0

Vértices: V.(0;2)

Eixo de simetria: x=0

Monotonia:

- É decrescente em x∈]-∞;0[ 

- É crescente em x∈]0;+∞[

Variação do sinal:

- A função é positiva em todo x∈R 

- A função não é nula (=0) e nem tem parte negativa. 

--------------------

5) $j(x)=x^2-3|x|+2$

Gráfico

Para construir o gráfico da função $j(x)=x^2-3|x|+2$ podemos nos basear nos seguintes passos:

1º Passo: Construir o gráfico (tracejado) de $y=x^2-3x+2$:

Lembre-se que: o gráfico de $y=x^2-3x+2$ é obtido pelos seguintes pontos de y=ax^2+bx+c:

Resolvendo temos: $x_1=1 ∨x_2=2; x_V=3/2=1,5 ; y_V=-1/4=-0,25$ e a ordenada na origem é o valor de $y=c=2$

2º Passo: Construir o gráfico de $j(x)=x^2-3|x|+2$  através de uma simetria em relação ao eixo das ordenadas (eixo y)

-- Isto significa fazer uma reflexão, em torno do eixo y, dos pontos do gráfico que possuem abcissa negativa.

Estudo completo:

Domínio: Dj=x∈R

Contradomínio: D^' j=y∈[-1/4; +∞[

Zeros: x={-2; -1; 1; 2}

A ordenada na origem é 2

Vértices: $V_1. (-3/2;-1/4);V_2. (0;2);V_3. (3/2;-1/4)$

Eixo de simetria: x=0

Monotonia:

- É decrescente em x∈]-∞;-3/2[ ∪ ]0;3/2[ 

- É crescente em x∈]-3/2;0[ ∪ ]3/2;+∞[

Variação do sinal 

- A função é positiva em em x∈]-∞;-2[ ∪ ]-1;1[ ∪ ]2;+∞[ 

- A função é nula (=0) em x={-2; -1; 1; 2}

- A função é negativa em x∈]-2;-1[∪ ]1;2[  

 

--------------------------