20 Exercícios Resolvidos de Teoria de Conjuntos

O que é Teoria de conjuntos?

Teoria de conjuntos é a teoria matemática que se dedica ao estudo da associação entre objetos ou elementos com a mesma propriedade. 

O que é um conjunto?

Conjunto é uma coleção bem definida de entidades ou objetos com a mesma propriedade.

Um conjunto é uma coleção de objetos com determinada característica comum. A cada objeto de um conjunto chama-se elemento do conjunto

Como é definido um conjunto?

Existem duas principais formas de escrever um conjunto: por extensão e por compreensão.

Na definição por extensão - os elementos são descritos de forma explícita dentro de chavetas e separados por vírgulas, ou no diagrama de Venn associados a um ponto. Enquanto na definição por compreensão, descreve-se a propriedade mais específica e comum dos seus elementos.

EXERCÍCIOS RESOLVIDOS 

1. Defina os seguintes
conjuntos por extensão.

N = {x| x é nome da províncias moçambicana que começa com a
letra n}.

Resolução: M= {Niassa; Nampula}

G = {x| x é divisor inteiros de 10};

Resolução: G= {-10; -5; -2;
0; 2; 5; 10}

H = {x| x é o conjunto dos múltiplos inteiros de 5};

Resolução: H= {…; -15;
-10; -5; 0; 5; 10; 15; ….}

I= {x: x é um número natural menor que 7}

Resolução: I= {0; 1; 2; 3;
4; 5; 6}

J={x: x é um número inteiro tal que -3<x≤5}

Resolução: J={-2; -1; 0;
1; 2; 3; 4; 5}

K= {x∈N:
x² ≤25}

Sabemos que
o único número natural cujo quadrado é 25, é o número 5. Por isso temos:

Resolução: K={x∈N:
x² ≤25} = { x∈N: x ≤5}={
0, 1, 2, 3, 4, 5}

 

2. Sendo A={1, 3, 4, 5, 6} e B={2, 4, 6, 8} determine:

2.1. A∪B                   2.2. A∩B

Resolução:

Resolução: 

2.1. A∪B = {1, 2, 3, 4, 5, 6, 8}

2.2. A∩B = {4, 6} 

3. Dados os conjuntos:

A = { x∈N: x ≤7} B
= { x∈Z: -4<x ≤4} e
C = { x∈N: x ≤9}
determine:

3.1. A                         3.2.
B             3.3.
C
3.4. A∪B       3.5. A∩B       3.6. (A∩B) ∪(B∩C)

Resolução:

3.1. A=
{0; 1; 2; 3; 4; 5; 6; 7}

3.2. B=
{-3; -2; -1; 0; 1; 2; 3; 4}

3.3. C=
{0; 1; 2; 3; 4; 5; 6; 7; 8; 9}

3.4. A∪B=
{-3; -2; -1; 0; 1; 2; 3; 4; 5; 6; 7}

3.5.
A∩B= {-3; -2; -1; 0; 1; 2; 3; 4; 5; 6; 7}

3.6. (A∩B)∪(B∩C)
= {0; 1; 2; 3; 4}∪{0; 1; 2; 3; 4; 5; 6; 7} = {0; 1;
2; 3; 4; 5; 6; 7}

4. Dados conjuntos: A= {-1,
0, 1, 2, 3, 4, 5} e B= {-1, 0, 2, 4, 5, 7},
assinale nas seguintes afirmações por V as verdadeiras e F as
falsas.

4.1. A∪B= {-1, 0, 2, 4}

4.2. A∩B= {-1, 0, 2, 4, 5}

4.3. A∩B= { }

4.4. (A∪B)∩A =A

4.5. (A∩B)∪B =B

Resolução:

4.1. F             4.2. V             4.3. F             4.4. V             4.5. V

 

5. Dado o diagrama abaixo, determine:

5.1. A              5.2.
B

5.3. C             5.4.
A∩B

5.5. A∪B       5.6. A∩B∩C

5.7. (A∩B)∪(B∩C)

5.8. n(A)       5.9.
n(A∩B)

5.10. n(A∪B)

Resolução:

5.1. A= {1; 2; 3; 4; 5}

5.2. B= {2; 5; 6; 7; 9}

5.3. C= {0; 2; 4; 6; 8}

5.4. A∩B=
{2; 5}

5.5. A∪B=
{1; 2; 3; 4; 5; 6; 7; 9}

5.6. A∩B∩C=
{2}

5.7. (A∩B)∪(B∩C)
= {2; 5}∪{2; 6} = {2; 5; 6}

5.8. n(A)=5

5.9. n(A∩B)=2

5.10. n(A∪B)=8

6. Dado o conjunto V = {a, e, i, o, u), determina o número máximo de subconjuntos que se podem formar.

Resolução:

Seja n o número de elementos e N o número de subconjuntos então temos: n=5 elementos; 

Sabemos que o N é dado por $N=2^n$. Então: $N=2^n=2^5=32$ Subconjuntos.

7. Dado o conjunto {1, 2, 3, 4, 5, 6, 7), qual é o
número máximo de subconjuntos distintos que se podem formar?

Resolução:
Seja n o número de elementos e N o número de
subconjuntos então temos: n=5 elementos;
Sabemos que o N é dado por $N=2^n$. Então: $N=2^n=2^7=128$ Subconjuntos.

8. Se um
conjunto A tem 1024 subconjuntos, determina o número de elementos do conjunto
A. E se tivesse 64 subconjuntos, quantos elementos teria o conjunto A?

Resolução:

Seja n o número de elementos e N o número de
subconjuntos então temos: N=64 elementos

Sabemos que o N é dado por  $N=2^n$.

 Então:$64=2^n$  ⇔ $2^4=2^n$   ⇔ $n=4$ elementos.

9. Dado o
conjunto {x∈R: x é raiz da equação x² - 4 = 0}, indica, em
extensão, os elementos desse conjunto.

Resolução:

Temos $x^2-4=0$ ⇔ $x^2=4$ ⇔ $x=±√4=±2$

Então: {x∈R: x é raiz da equação x² - 4 = 0} ={-2;2}

10. Dados os
conjuntos A= (2, 4, 6), B = {x: x é par} e C = {1, 3, 5, 7}, classifica como
verdadeiras ou falsas as afirmações seguintes:

10.1  2∈A

10.2  7∈C

10.3  A⊂B

10.4  B⊂A

10.5  {1; 7}⊄C

10.6  {2; 4}⊄B

10.7  A⊄C

10.8
{2.4.6} ⊂ (B∩C).

Resolução:  

10.1. V           102.V
            10.3 V             10.4 F

 10.5  F           10.6 F             10.7 V            10.8.F

11. A intersecção dos conjuntos
{x: x é par e menor que 9) e {1,3,5,7} é (escolhe a opção correta.):

a) (2)

b) { }

c) (2,3)

d) {1,2,3,4,5,6,7,8)

Resolução:

No conjunto {1,3,5,7} Não temos nenhum número par, então a intersecção
destes conjuntos é vazia. Resposta: b) { }

 

12. Sendo A e B dois
conjuntos não vazios e A ⊂B, qual das seguintes afirmações é verdadeira?

a) A∩B=B

b) A∪B=B

c) A∩B = { }

d) A∪B = { }

Resolução:

A intersecção de um conjunto com o seu subconjunto é o próprio
subconjunto, enquanto a união de um conjunto com o seu subconjunto é o próprio
conjunto. Resposta: a) A∩B=B

 

13.
Um grupo de 35 turistas visitou algumas praias de Moçambique. 16 turistas
visitaram apenas a praia do Wimbe e 11 apenas a praia de Tofo. Quantos turistas
visitaram ambas as praias?

Resolução: consideremos x o número de turistas visitaram ambas as praias, e
representando os dados no diagrama de Venn temos:

x=?   16+x+11=35 

⇔ 27+x=35

⇔x=35-27 ⇔ x=8

Resposta:
O número de turistas visitaram ambas as praias é 8.

14. Numa vila da província de Maputo, 25% dos habitantes sabem
conduzir automóvel, 40% sabem conduzir motorizada e 12% sabem conduzir os dois
tipos de veículos.

14.1 Qual é a percentagem
de habitantes que não sabe conduzir nem automóvel nem motorizada? Representa a
situação num diagrama de Venn.

Resolução:

Apenas automóvel
=25%-12%=13%

Apenas motorizada
=40%-12%=28%

x=?
23+12+15+x=100 

⇔ 53+x=100 

⇔x=100-53 ⇔  x=47

Resposta:
A percentagem de habitantes que não sabe conduzir nem automóvel
nem motorizada é de 47%

 

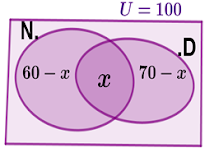
15. Numa escola
secundária da cidade de Pemba, 60% dos alunos leem o Jornal Notícias, 70% leem
o jornal Diário de Moçambique, e todos os alunos leem pelo menos um dos
jornais.

15.1
Qual é a percentagem dos alunos que leem os dois jornais?

Resolução: Seja
x a intersecção (percentagem
dos alunos que leem os dois jornais), temos:

 Apenas Jornal Notícias=60-x

Apenas Jornal Diário
=70-x

x=?
(60-x)+x+(70-x)=100 

⇔ 60-x+x+70-x=100  

⇔ 130+ x=100 

⇔ -x=100-130 

⇔ -x=-30 ⇔ x=30

Resposta:
A percentagem dos alunos que leem os dois jornais é de 30%

16. Perguntaram a 165 alunos de uma Escola
Secundária sobre as suas preferências musicais e o resultado foi o seguinte:

⚫ 65 alunos disseram que gostavam de
Marrabenta;

⚫ 74 disseram que gostavam de música Afro
jazz; 63 disseram não gostar destes dois géneros musicais.

16.1. Quantos alunos
gostam de Marrabenta ou Afro jazz?

Resolução: Quando
diz-se “ou” significa uma união, isto é alunos que gostam de, pelo menos, uma
das partes: Esse número pode ser obtido subtraindo os que não gostam de nenhum
género musical no universo: M∪A=165-63=102.

Resposta:
O número dos alunos que gostam de Marrabenta ou Afro jazz
é de 37.

16.2. Quantos alunos
gostam de ambos géneros (Marrabenta e Afro jazz)?

Resolução: Seja
x a intersecção (alunos que
gostam de ambos géneros musicais), temos:

 Apenas Marrabenta =65-x

Apenas Afro jazz =74-x

x=?
(65-x)+x+(74-x)+63=165 

⇔ 65-x+x+74-x+63=165 

⇔  202+
x=165 

⇔ -x=165 -202 

⇔  -x=-37 ⇔  x=37

Resposta:
O número dos alunos que gostam de ambos é de 37.