(PDF) Dosificação de matemática 11ª classe

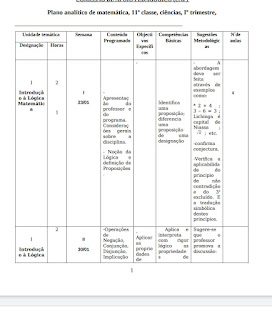
Plano analítico de matemática, 11ª classe, ciências Iº trimestre

A planificação de uma aula é um dos conteúdos da disciplina de Psicopedagogia. Como é sabido, as disciplinas de formação de professores relacionam-se entre si. É desta forma que o sítio de ensino pretende ajudar os caros docentes do ensino secundário principalmente os da matemática.

Dosificação ou plano de analítico dos conteúdos do programa de ensino de matemática?

Deste modo não deve constituir uma dificuldade o aparecimento deste assunto na Didáctica da Matemática. Aqui, este assunto não será tratado na sua íntegra pois o que interessa é o modelo de uma dosificação para a disciplina de matemática 11ª classe sessão de ciências.

Nota: O nosso objectivo não é criar a preguiça nos professores mas sim dar um apoio aos novos na carreira. De lembrar que você pode deixar o seu comentário abaixo em casos de uma qualquer anomalia na dosificação ou em casos de sugestões.

PARA VISUALIZAR NO ANDROID MUDE O SEU NAVEGADOR PARA O MODO COMPUTADOR

PLANO ANALÍTICO DE MATEMÁTICA, 11ª CLASSE, CIÊNCIAS, Iº TRIMESTRE, modelo baseado no ano lectivo de 2017

Solicitar todas as dosificações em👉 pdf

Unidade temática				Semana	Conteúdo Programado	Objectivos Específicos	Competências Básicas	Sugestões Metodológicas	N°de aulas
Designação		Horas
I Introdução à Lógica Matemática		2 1		I 23/01	-Apresentação do professor e do programa. Considerações gerais sobre a disciplina. - Noção da Lógica e definição de Proposições.	-	Identifica uma proposição; diferencia uma proposição de uma designação	- A abordagem deve ser feita através de exemplos como: * 2 + 4   ;  3 – 6 = 3 ; Lichinga é capital de Niassa ; ;  etc. -confirma conjectura. -Verifica a aplicabilidade do  principio de não contradição e do 3o excluído. E a tradução simbólica destes princípios.	4
I Introdução à Lógica Matemática		2 1 1		II 30/01	-Operações de Negação, Conjunção, Disjunção, Implicação e Equivalência de proposições. -Tabelas de verdade. - Exercícios.	- Aplicar as propriedades de negação, disjunção e conjunção	Aplica e interpreta com rigor lógico as propriedades de negação, conjunção, disjunção e as leis de Morgan na resolução de problemas concretos.	Sugere-se que o professor promova a discussão: -- Termo ou designação e proposição. -Proposição e expressão proposicional.  Expressão designatoria e expressão proposicional.	3
I Introdução à Lógica Matemática		1 1 1		III 06/02	-Propriedades da Negação, Conjunção e Disjunção. - 1as Leis de Morgan. - Exercícios.	-Demonstrar as propriedades através da tabela de verdade; - Interpretar as 1as leis de Morgan	“	“	4
I Introdução à Lógica Matemática		1 1 1 1		IV 13/02	-Expressões proposicionais - Exercícios -Quantificação e Quantificadores Universal e Existencial -2as Leis de Morgan.	- Distinguir expressão proposicional de uma proposição; - Aplicar quantificadores na tradução de expressões quantificadas e vice-versa; - Interpretar as 2as leis de Morgan	Usa quantificadores na tradução de expressões correntes em expressões quantificadas e vice-versa; Aplicar as leis de Morgan na resolução de problemas concretos. Usa conhecimentos da lógica como via para disciplinar a mente e exercitar capacidade de comunicar conceitos, raciocínio e ideias com clareza.	- A abordagem deve ser feita através de exemplos como: * 3 + x   ; 3 + x = 8 ; ;  etc. Sugere-se que o professor oriente os alunos a traduzirem para a linguagem corrente expressões quantificadas e vice-versa	4
I Introdução à Lógica Matemática		1 1 1 1		V 20/02	-Exercícios sobre Quantificadores - 1º Teste escrito - Indução Matemática. - Exercícios	-Explicar e aplicar o método de demonstração por indução matemática. .	-                             “	O propor propriedades, teoremas, … de casos simples para demonstração do método de indução.	4
II Álgebra		1 1 1 1		VI 27/02	-Expressões algébricas: definição e classificação. - Exercícios -Domínio de existência de expressões Racionais - Exercícios	- Distinguir uma expressão algébrica da não algébrica; - Classificar as expressões algébricas -Determinar o domínio de existência duma expressão racional	-Identifica e classifica expressões algébricas.	Sugere-se que o professor proponha varias expresses para a selecção conforme as semelhanças e dai concretizar. - Propor exercícios de determinação de domínio de expressões com exemplos simples	4
II Álgebra		1 1 1 1		VII 06/03	-Domínio de existência de expressões Irracionais - Exercícios -Transformações idênticas. - Entrega e correcção do 1 a Teste escrito	-Determinar o domínio de existência duma expressão Irracional	- Interpreta o significado das regras no contexto de situações concretas na determinação de Domínio de existência	“	4
II Álgebra		2 2		VIII 13/03	-Fracções racionais: definição, Domínio de existência e -simplificação de fracções racionais. -Exercícios	-Identificar uma fracção racional, determinar o seu domínio de existência; -Simplificar fracções racionais.	-Representa relações funcionais de diferentes maneiras, passando de um tipo de representação para outros usando regras verbais, tabelam, gráficos e expressões algébricas;	“	4
II Álgebra		2 2		IX 20/03	-Operações com Fracções Racionais. -Exercícios	Operações com fracções racionais (+ ; - ; x ;  e : )	“	Sugere-se que o professor use o teorema do resto, regra de Ruffini na simplificação de fracções	4
II Álgebra		1 2 1		X 27/03	-Expressões Irracionais: Definição e racionalização do denominador. Exercícios. -Equações: definição; Equivalência de equações. Exercícios	- Identificar uma expressão irracional, -Racionalizar os denominadores -Identificar equações equivalentes;	“	Segure-se que o professor coloque modelos de exercícios mais simples                   “	4
II Álgebra		2 2		XI 03/04	Avaliação Trimestral				*3
				XII 10/04	- Entrega e correcção das avaliações Considerações finais do trimestre e divulgação das notas.
			Imagem de exemplo em pdf

Modelo Dosificação ou plano de analítico dos conteúdos em pdf

Modelo de Dosificação ou plano de analítico dos conteúdos em Moçambique pdf.

Modelo de Dosificação ou plano de analítico dos conteúdos em pdf

Dosificação ou plano de analítico dos conteúdos em pdf

Para mais informações consulte os programas de ensino secundário

Dosificações dos conteúdos do programa, 11ªclasse, 10ª classe, 12ª classe, 9ª classe E 8ª classe em pdf.

Dosificações dos conteúdos do programa, 1ªclasse, 2ª classe, 3ª classe, 4ª classe 5ªclasse, 6ª classe 7ª classe emPDF

Fonte: PROGRAMAS DE ENSINO SECUNDÁRIO.

Para mais informações consulte os programas de ensino secundário

Dosificações dos conteúdos do programa, 11ªclasse, 10ª classe, 12ª classe, 9ª classe E 8ª classe em pdf.

Dosificações dos conteúdos do programa, 1ªclasse, 2ª classe, 3ª classe, 4ª classe 5ªclasse, 6ª classe 7ª classe emPDF